문제 요약
문제 링크: 백준 24232 - 망가진 나무
문제 설명

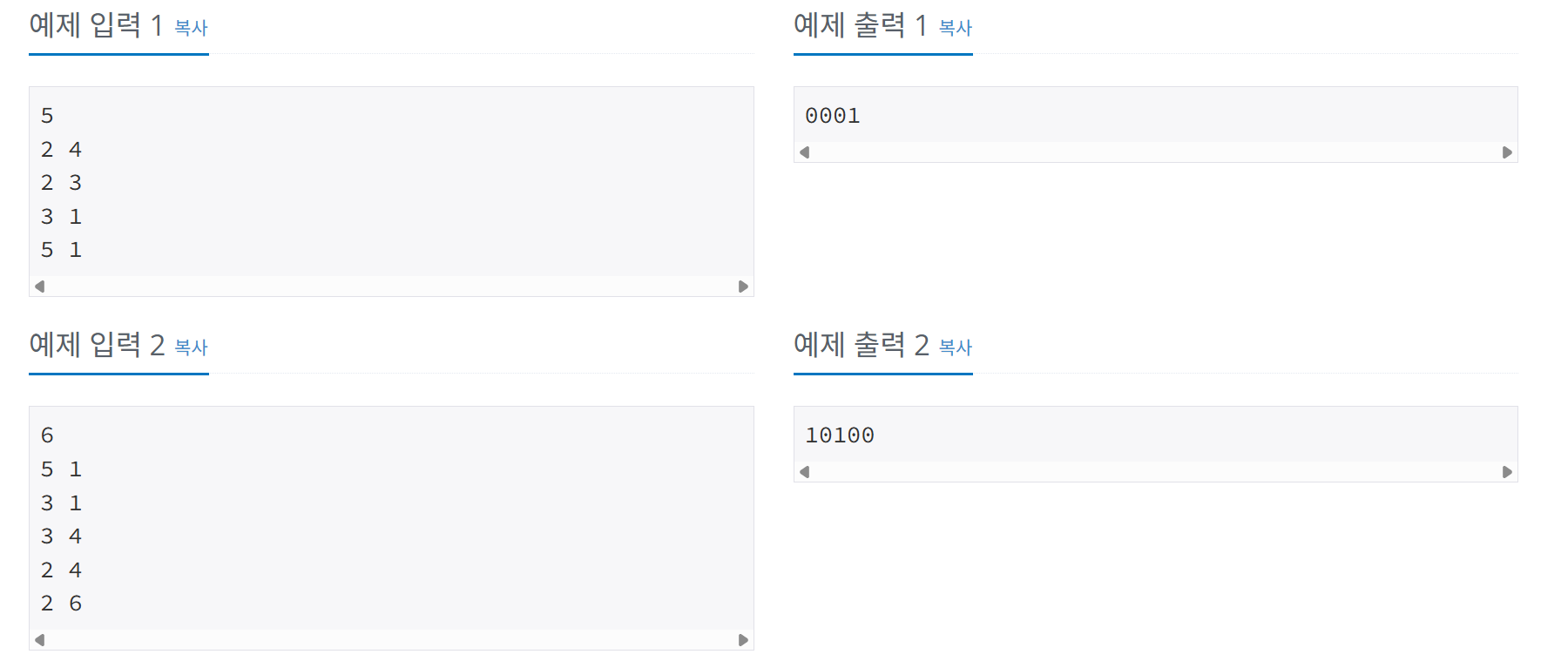
접근 방법
문제에서 주어진 입력을 무방향 그래프로 구성하면 트리 구조를 가지는 그래프가 된다.
예제1의 경우를 그림으로 살펴보면

이렇게 된다. 간선마다 번호가 있다는 것에 유의하자
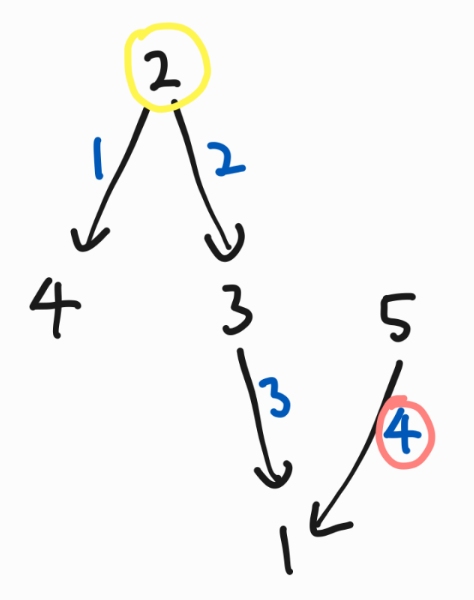
예제 1번은 노란색 정점(2번)에서 시작하면 4번 간선만 뒤집게 된다면 트리 구조, 즉 2번 정점에서 출발하여 모든 정점에 도달 가능한 형태가 된다.
1. 우선 임의의 정점에서 그래프의 방향을 신경쓰지 않고 모든 정점에 도달할 때 까지 몇 번 간선을 뒤집어야 하는지 세준다. (DFS 첫번째 탐색)
2. 정점을 모두 돌며 세준 값을 기준으로 다시 해당 임의의 정점부터 모든 정점까지 탐색을 해주는데, 이때 간선이 존재한다면(임의의 정점에서 자식으로 간선이 존재하고 방향이 올바르다면) dp 값을 갱신해준다.
이 한 번의 O(N) 탐색으로, 임의 노드부터 모든 노드 i가 루트일 때의 총 뒤집기 횟수를 효율적으로 모두 계산할 수 있다.
3. dp로 체크한 가장 적은 뒤집기 횟수를 가지는 루트 노드로 시작하여, 간선의 번호를 신경쓰며 뒤집어야 할 간선을 마킹해주는 DFS(세 번째 DFS)로 문제를 해결할 수 있다.
코드
#include <bits/stdc++.h>
using namespace std;
int n, cnt;
vector<int>v[100001];
map<pair<int, int>, bool>m;
map<pair<int, int>, int>edge;
int dp[100001], ans[100001];
void dfs(int x, int par) {
for (int i:v[x]) {
if (i != par) {
if (m[{x, i}] != 1)
cnt++;
dfs(i, x);
}
}
}
void dfs2(int x, int par) {
for (int i : v[x]) {
if (i != par) {
if (m[{i, x}] == 1)
dp[i] = dp[x] - 1;
else
dp[i] = dp[x] + 1;
dfs2(i, x);
}
}
}
void dfs3(int x, int par) {
for (int i : v[x]) {
if (i != par) {
if (m[{x, i}] == 1)
ans[edge[{x, i}]] = 0;
else
ans[edge[{i, x}]] = 1;
dfs3(i, x);
}
}
}
void solve() {
dfs(1, 0); // 임의 정점 시작
dp[1] = cnt;
dfs2(1, 0);
int mn = 1e6, start;
for (int i = 1; i <= n; i++) {
if (mn > dp[i]) {
mn = dp[i];
start = i;
}
}
dfs3(start, 0);
for (int i = 0; i < n - 1; i++) cout << ans[i];
}
void input() {
cin >> n;
for (int i = 0; i < n - 1; i++) {
int a, b;
cin >> a >> b;
v[a].push_back(b);
v[b].push_back(a);
m.insert({ {a,b},1 });
edge.insert({ {a,b},i });
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
input();
solve();
}'백준 문제풀이 > dfs' 카테고리의 다른 글
| [BOJ] 23887 프린트 전달 (0) | 2025.10.19 |
|---|---|
| [BOJ] 14657 준오는 최종인재야!! (0) | 2025.10.05 |
| [BOJ] 1035 조각 움직이기 (0) | 2025.09.17 |